深度学习入门笔记(二)
从逻辑回归到神经网络
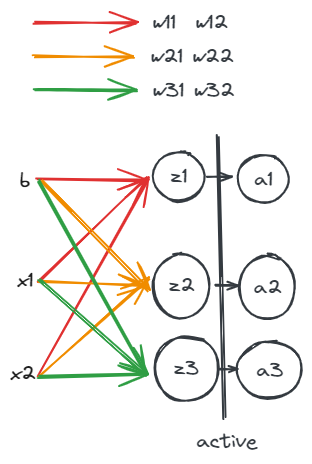
上文学习了逻辑回归的基本计算方法,神经网络相当于是对逻辑回归模型的一个扩展。首先是纵向扩展,如图所示:
输入特征为$x_1, x_2$,偏置为$b$,第一层计算为:
\[z_1=x_1*w^{[1]}_1+x_2*w^{[1]}_2+b\] \[a_1=g(z_1)\]这里函数$g(x)$是激活函数,而上标表示第1层的参数。同理:
\[z2=x_1*w^{[2]}_1+x_2*w^{[2]}_2+b\] \[a2=g(z2)\] \[z3=a1*w^{[3]}_1+a2*w^{[3]}_2+b\] \[a3=g(z3)\]每个$z$都是一个逻辑回归中的计算过程。此时作为参数的$w$被纵向扩展,从
\[\begin{bmatrix} w_1^{[1]} , w_2^{[1]} \\ \end{bmatrix}\]扩展到了
\[\begin{bmatrix} w_1^{[1]} , w_2^{[1]} \\\\ w_1^{[2]} , w_2^{[2]} \\\\ w_1^{[3]} , w_2^{[3]} \\\\ \end{bmatrix}\]向量化这个计算方法就是:
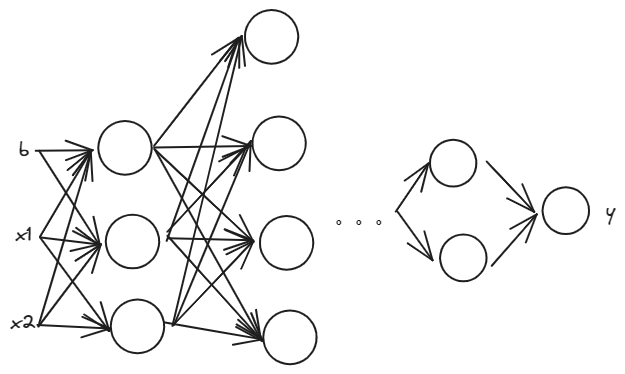
\[Z^{[1]}=W^{[1]}X+b^{[1]}\] \[A^{[1]}=g(Z^{[1]})\]然后是横向扩展,相当于上图横向加深深度,这个网络就叫做神经网络,如图所示:
神经网络训练
前向计算比较简单,很直观的扩展逻辑。而反向计算求梯度较为复杂,简单描述步骤如下:
- 损失函数$Loss(y, \hat{y})$对$\hat{y}$的求导,这个是比较简单的,求得的值为$da^{[L]}$。
最后一次的激活函数求导:
\[\frac{dLoss}{dz^{[L]}}=da^{[L]}*g^{[L]'}(z^{[L]})\]这里的$g^{[L]’}(z^{[L]})$是激活函数的导数, $da^{[L]}$是损失函数的导数,根据链式法则可以求得损失函数对$z^{[L]}$的导数。($L$表示神经网络的层数,从1~$L$)
通过$dz^{[L]}$可以求得$dw^{[L]}$和$db^{[L]}$,然后通过$dw^{[L-1]}$和$db^{[L-1]}$可以求得$dz^{[L-1]}$,以此类推,直到求得$dw^{[1]}$和$db^{[1]}$。具体如下:
\[dw^{[L]}=dz^{[L]}*a^{[L-1]T}\] \[db^{[L]}=dz^{[L]}\] \[dz^{[L-1]}=w^{[L]T}*dz^{[L]}*g^{[L-1]'}(z^{[L-1]})\]这里值得注意的是,前向计算都是$Z^{[L]}=W^{[L]}A^{[L-1]}+b^{[L]}$,而反向计算都是与参数矩阵的转秩进行计算.
- 通过梯度下降法更新各个层的参数$w$和$b$。
从一次训练到多次训练
这里相当于再次升维。
特征值的变化
首先看输入,单词训练的输入特征矩阵为:
\[\begin{bmatrix} x_1^{(1)} \\\\ x_1^{(2)} \\\\ \vdots \\\\ x_1^{(m)} \\\\ \end{bmatrix}\]扩展为多次训练后,矩阵变为:
\[\begin{bmatrix} x_1^{(1)} & x_2^{(1)} & \cdots & x_n^{(1)} \\\\ x_1^{(2)} & x_2^{(2)} & \cdots & x_n^{(2)} \\\\ \vdots & \vdots & \ddots & \vdots \\\\ x_1^{(m)} & x_2^{(m)} & \cdots & x_n^{(m)} \\\\ \end{bmatrix}\]矩阵的维度变为:$n*m$,这里的$m$表示训练的次数,$n$表示特征的数量。
参数变化
参数矩阵是没有发生变化的,为什么呢?因为参数矩阵是在训练过程中不断更新的,而不是在训练次数上发生变化的。可以分析一下,特征矩阵的维度为$n1$时,假设第一层的神经网络节点为$n^{1}$个,那么参数矩阵$W$的维度为$L^{1}n$,这样第一层节点的计算$A^{1} = WX+b$,得到第一层节点的矩阵为$L^{1}1$。
当输入扩展到$nm$时,参数矩阵$W$的维度为$L^{1}n$,这样第一层节点的计算$A^{1} = WX+b$,得到第一层节点的矩阵为$L^{1}m$。这里的$m$表示训练的次数,而不是参数矩阵的维度。
损失函数的变化
多次训练后,损失函数为单次损失函数的求和,即:
\[Loss(y, \hat{y})=\frac{1}{m}[Loss(y^{(1)}, \hat{y}^{(1)})+Loss(y^{(2)}, \hat{y}^{(2)})+\cdots+Loss(y^{(m)}, \hat{y}^{(m)})]\]可以用$\sum$表示为:
\[Loss(y, \hat{y})=\frac{1}{m}\sum_{i=1}^{m}Loss(y^{(i)}, \hat{y}^{(i)})\]梯度下降法的变化
梯度下降法的变化也很简单,就是将单次训练的梯度下降法扩展到多次训练,即:
\[W=W-\alpha\frac{1}{m}\sum_{i=1}^{m}\frac{\partial Loss(y^{(i)}, \hat{y}^{(i)})}{\partial W}\]浅神经网络VS深神经网络
这里的深浅意思是神经网络的层数,实践表明更高的深度以为着更丰富的表达,训练的结果也更好,所以现在深度神经网络变成主流,也获得了巨大的成功。
总结
从逻辑回归推导到神经网络就是一个不断升维并向量化的过程,计算量指数级上涨,但是计算方法基本不变。可以脑部一下,如果是这样一个神经网络,他的计算量相关的点有以下几个:
- 输入特征的数量,这个决定了矩阵乘法的列数,一般来说隐藏层每一层的节点数是输入特征的数量的倍数。不会低于输入特征的数量。
- 单次训练的次数,这个决定了矩阵乘法的行数,也就是神经网络的深度。
- 神经网络的层数,这个决定了矩阵乘法要进行的次数,也就是神经网络的宽度。
与网络相关的思考
假设第L层的参数规模为$W^{L}$为$\begin{bmatrix} L, L-1 \end{bmatrix}$,那么该层的浮点数计算量为$LL-1Lm$,其中$m$表示训练的次数。不妨假设每一层的节点数相当,那么整个神经网络的计算量为$L^2mcnt$。$cnt$为神经网络的层数,总的参数量为$L^2cnt$。反向计算的计算次数比正向多一个乘法(因为要乘上传递过来的梯度)。但是不额外产生参数了。在做梯度聚合时,需要同时传递所有参数,假设参数为7B,那么单次通信量就为7B,但是由于并行策略,做了流水线并行的情况下,单个主机并不会拥有所有参数,可能实际在做梯度聚合时通信量会打个折扣。具体的计算方法还需要再学习学习。