深度学习入门笔记(一)
动机
由于工作需要,以后的精力主要放在AI相关的领域上,尤其是现在大火的深度学习。我关注的领域是网络,目前深度学习对网络的需求还是非常苛刻的,苛刻的原因与深度学习的特性有关。为了让AI模型更加强大,模型使用了越来越大规模的参数,而超大规模的参数做矩阵乘法带来的超大计算量以及大量的GPU内存开销,让深度学习的系统不得不成为一个大型分布式系统。
当前深度学习训练过程依赖这个分布式系统,而当前的训练框架容错能力都非常差,以至于分布式系统中的任意故障都会导致训练业务中断。网络作为连接大型分布式系统的基础设施,在这种敏感的系统中尤为关键,现在已知的几个方面是研究的重心:
- 网络拓扑
- 网络协议
- 拥塞控制
- 负载均衡
- 终端带宽
而对应的问题有一下这些:
- 二层胖树网络可扩展性差,无法支撑更多节点;三层CLOS网络可扩展性好,配置复杂
- 终端无法感知拓扑,容易导致跨汇聚通信增加延时
- 网络丢包或者高延迟会被认为是通信故障,采用IB成本高,而RoCEv2缺陷很多
- 基于ECN的拥塞控制响应滞后,也无法更精准的流控
- all-reduce导致的大象流让ECMP失效
- 为了防止拥塞,需要终端上要求400G的接入,如果有更高的接入带宽则网络拓扑可以更轻松的扩展
可以看到这些问题都不是网络本身产生的问题,几乎都是业务属性导致的问题,因此了解业务本身是解决这些业务需求的一个关键。毕竟业务不会一成不变,网络也要考虑演进适配。
学习资料
我是跟着吴恩达老师学习的,具体地址在吴恩达老师的深度学习课程,本文是1-20节的学习心得感悟。
另外,在看视频前,我粗浅的读了一遍 :《深度学习入门》 这本书在讲的也挺好的
深度学习是什么
首先梳理下脉络,在《深度学习入门》 里面提到了感知机,这个是深度学习的原型,如下图所示 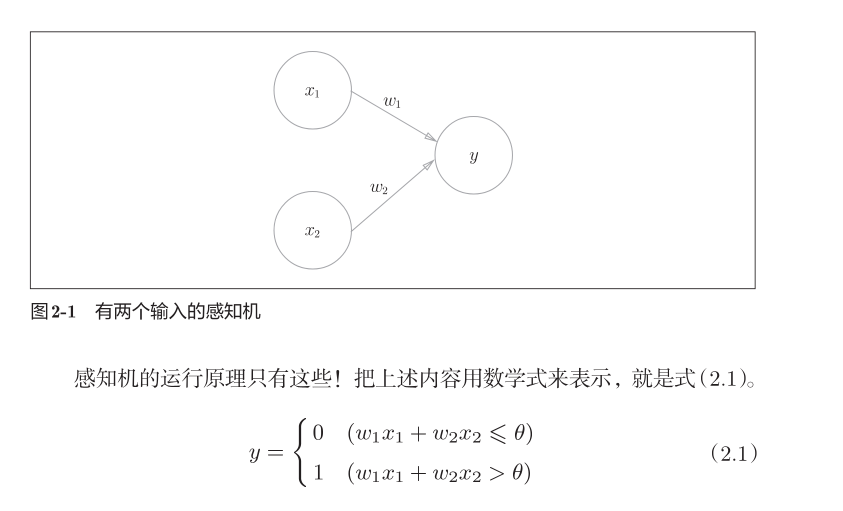
简单的看一眼就能清楚,这个感知机可以用来实现与或非门之类的门电路。神经网络就是有很多很多这样的感知机组成的,一个简单的神经网络如图:
深度学习是一种方法,而利用神经网络进行深度学习是现在最主流的方法,其他方法还有决策树,随机森林什么的,这里不讨论了。
从逻辑回归开始
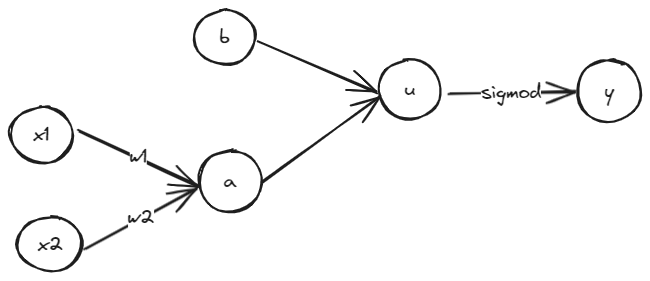
深度学习还是比较复杂的,他可以实现很多模型,一个比较简单的模型是逻辑回归,逻辑回归是用来做二元分类的,比如判断一张图片里面是不是画了一只猫这种,逻辑回归的基本流程可以简单如下图:
假设这是一个只有2个参数的模型,可以这样描述这个模型:
- $w_1,w2$就是参数,其中$x1,x2$是需要进行推理的输入特征(如果是图片那么可能是每个像素点的RBG值)
- $a$是一个中间值可以是$a = x_1 \cdot w_1 + x_2 \cdot w_2$
- $u=a+b$
- $y=\sigma(u)$ (其中,$\sigma(x)= \frac{1}{1 + e^{-x}}$)
最终,$y$表示传入的这个$x1,x2$算出来的$y$是1的概率,回到示例上就是说这张图有多大概率是猫。以上就是逻辑回归是如何根据传入特征进行分类的算法,这就是深度学习经常说的前向计算。
如何优化逻辑回归模型
我们已经有了一个模型可以计算出输入特征是猫的概率了,但是如果我们传入一张猫图的特征后得到的概率太低怎么办,而我们传入非猫图片时得到的概率太高又怎么办,解决这个的方法就是所谓的训练。
训练过程可以这么认为,我们为逻辑回归模型设置一个默认的参数矩阵$W$,每次通过输入$X$可以计算出一个分类值$Y$,通过定义一个损失函数$\hat{Y}$,尝试使用梯度下降法调整$W$,使得$Y$和$\hat{Y}$之间的差值最小。
最终这一组$W$就是我们训练好的模型,可以用来进行分类了。 具体如下:
设置基础参数
- 输入特征为$X = \begin{bmatrix} x_0 \\ x_1 \\ … \\ x_n \end{bmatrix}$
- 参数为$W = \begin{bmatrix} w_0 \\ w_1 \\ … \\ w_n \end{bmatrix}$
- 输出为$Y = W^T \dot{X}$ + b
损失函数
我们可以设置一个损失函数$\hat{Y}$,令$\hat{Y} = Y$,那么损失函数可以表示为:$L = \frac{1}{2}(Y - \hat{Y})^2$,这个损失函数表示的是$Y$和$\hat{Y}$之间的差值的平方,这个差值越小,损失函数越小。但是由于这个方差函数不是凸函数,无法使用我们常用的梯度下降法来进行优化,所以通常可以使用另外一个损失函数: $L = -\hat{Y} \cdot log(Y) - (1 - \hat{Y}) \cdot log(1 - Y)$
梯度下降法
不妨令:
- $u=W^T \dot{X} + b$
- $Y = \sigma(u)$
- $\hat{Y} = L(Y) $
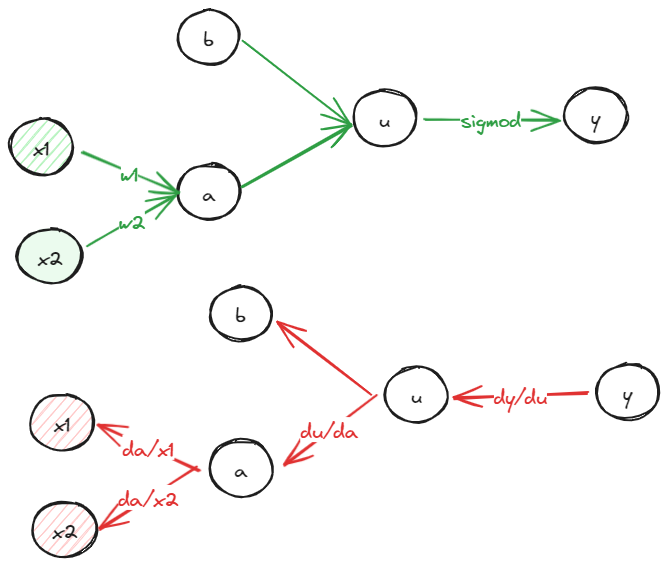
我们通常利用导数的链式法则,反过来求解梯度,也被成为反向传播。
为了使得$\hat{Y}$变小,这个导数可以表示为:$d\hat{Y} = \frac{\partial L}{\partial Y} \cdot \frac{\partial Y}{\partial u} \cdot \frac{\partial u}{\partial W}$。
而$W$是一个参数矩阵$\frac{\partial u}{\partial W}$本质上是对于$W$的偏导数,可以理解为$u=x_1 \cdot w_1 + x_2 \cdot w_2 + … w_n \cdot x_n+ b$,对于各个不同的$w$求导,由于有n个$w_i$,所以最终求得的偏导数可以表示为:$\begin{bmatrix} d_1 \\ d_2 \\ … \\ d_n \end{bmatrix}$。 梯度下降法可以表示为:
- $W = W - \alpha \cdot \frac{\partial L}{\partial W}$
- $W = W - \alpha \cdot \begin{bmatrix} d_1 \\ d_2 \\ … \\ d_n \end{bmatrix}$ =>
- $W = \begin{bmatrix} w_0 \\ w_1 \\ … \\ w_n \end{bmatrix} - \alpha \cdot \begin{bmatrix} d_0 \\ d_1 \\ … \\ d_n \end{bmatrix}$
这里的$\alpha$是学习率,意思就是参数需要往这个方向调整的程度。 附上老师的板书: 
为什么要求导数,因为导数是函数在某个值的的斜率,对于凸函数来说函数变量加上它的导数就是函数值更大,而减去它的导数就会函数值变小
批次训练与迭代
每次训练都是使用当前的训练数据的特征输入,以及训练标签获得损失函数,通过损失函数获得各个参数的梯度。一次训练m组数据则需要将m次的梯度相加求平均,然后再做梯度下降。使用不同批次的数据多次迭代则最终可以获得一个可用的参数组合,也就是我们训练出来的模型的参数了。
总结
这篇笔记主要是阅读了《深度学习入门》,以及Youtube上的吴恩达老师的深度学习课程的1-20节的学习心得感悟。通过对逻辑回归计算方法说明了前向计算主要是通过特征与参数做矩阵乘法以及激活函数来完成的。而反过来利用参数求损失函数的偏导以及梯度下降优化参数的过程则是被成为反向传播。